StatCalc: Statistical Calculators
‹View Table of Contents
Stratified Analysis of 2 x 2 Tables
Stratifying a dataset separates the population into distinct categories based on levels of a parameter (i.e., sex). If confounding is present, associations between disease and exposure can be missed or falsely detected. A confounding factor is one that is associated with the disease and the exposure, but may not be of interest or observed. Age is a frequent confounder, although any factor other than the main exposure being considered can be treated as a confounder.
Stratification means making a separate table of disease by exposure for each possible confounder combination. In the simplest case, this could mean separate male and female tables if sex is the potential confounder. If age, sex, and city are confounders, separate tables will be made for each possible combination of age group, sex, and city.
The Mantel-Haenszel weighted odds ratio, risk ratio, summary chi square, and p-value calculations combine results from different strata to remove confounding caused by the variables used for stratification. If tables are created for male and female, confounding by sex is removed. The degree of confounding can be judged by comparing the crude and weighted odds ratios. If the ratios are identical, there was no confounding by sex.
The Adjusted Mantel-Haenszel and Adjusted Mantel-Haenszel confidence limits provide additional measures. If the weighted odds ratio or risk ratio (not for case-control studies) has confidence limits that do not include 1.0, there is a statistical association with 95% confidence between the disease and the exposure without confounding by the stratifying factor.
If the odds ratio or risk ratios for strata in a series of stratified tables for the tests are not similar, then interaction between the stratifying factor and the risk factor are present.
Example
The following example investigates the relationship between alcohol and myocardial infarction (Relationship Between Alcohol Consumption and Myocardial Infarction (MI): Confounding Due to Smoking Hypothetical Data, Schlesselman JJ. Case-control studies. New York: Oxford University Press, 1982).
The following case-control study indicates an apparent association between alcohol consumption and MI.
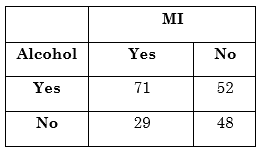
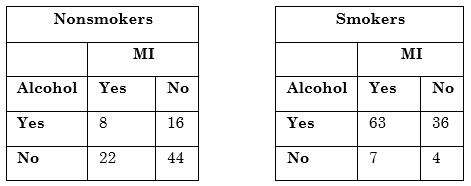
Smoking is known to be associated with MI and alcohol consumption. Stratifying the data by smoking status creates two tables, one for smokers and one for nonsmokers.
To view and create a stratified analysis:
- From the StatCalc application main page, select Tables (2 x 2, 2 x n). A blank table opens in the StatCalc application window.
- Enter the data from the Nonsmokers sample table in the Strata 1 tab.

- Click the Strata 2 tab.
- Enter the data from the above Smokers sample table.
- The summary results populate as you enter data.
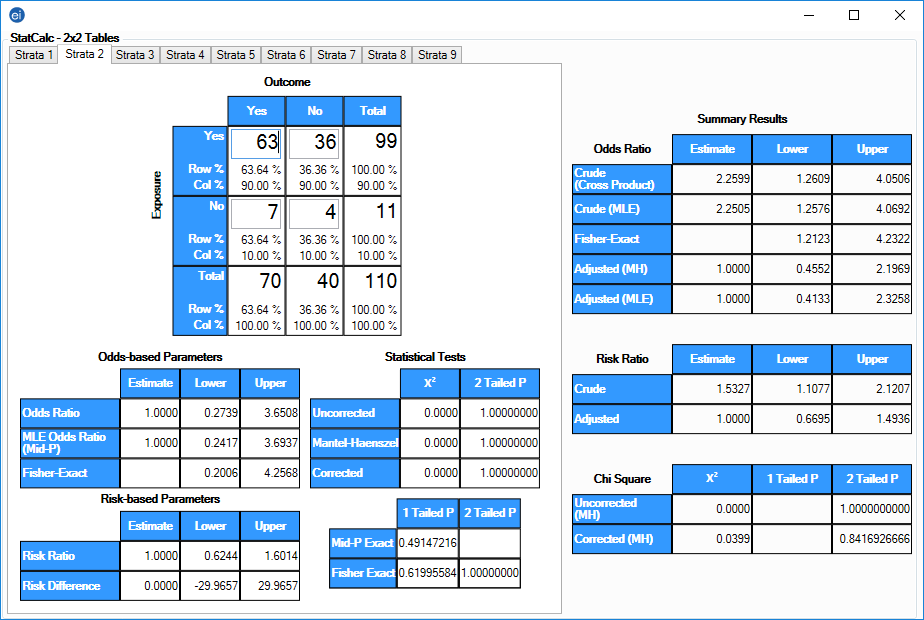
The odds ratio for each table is 1.0, and the Mantel summary adjusted odds ratio is 1.0. The crude odds ratio and the Mantel-Haenszel summary odds ratio are quite different (2.26 and 1.0), concluding that smoking was a confounding factor and there appears to be no association (odds ratio = 1.0) between alcohol and MI in this example. Note that the odds ratio in the two strata is the same (1.0). There is no interaction or effect modification between smoking and alcohol. In other words, the effect of alcohol on MI is the same for smokers and nonsmokers. When the effect varies in the different strata (the odds ratios are different), interaction or effect modification is present.
Note: Summary results only appear in stratified data sets (summary results show adjusted results based on the stratification criteria).