Hypothesis Testing when using the NHANES-CMS linked data
Purpose
The t-test and chi-square statistics are used to test statistical hypotheses about population parameters. This module will demonstrate the use of these statistics in NHANES data analysis.
Task 1: Use the t-test statistic
The t-test is used to test the null hypothesis that the means or proportions of two population subgroups are equal OR that the difference between two means or proportions equals zero when the estimates are based on a small probability sample. When using a simple random sample, small is defined as less than 30.
The t-test is used to test the null hypothesis that two population means or proportions, θ1 and θ2, are equal OR, equivalently, that the difference between two population means or proportions is zero. To test this hypothesis, assuming the covariance is small, as is the case with NHANES data, the following formula is used
Equation for t-Test Where Covariance is Small
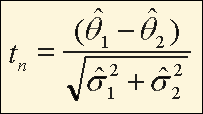 (1)
(1)
where,
![]() 1 is an estimate of θ1 based on a probability sample,
1 is an estimate of θ1 based on a probability sample,
![]() 1 is an estimate of the standard error of
1 is an estimate of the standard error of ![]() 1,
1,
![]() 2 is an estimate of θ2,
2 is an estimate of θ2,
and ![]() 2 is an estimate of the standard error of
2 is an estimate of the standard error of ![]() 2.
2.
In instances where the t statistic is based on a small number of independent pieces of information (i.e. a small number of degrees of freedom [<30]), the statistic given in equation 1 follows a Student’s t distribution with mean=0 and unit variance with n degrees of freedom. In the NHANES 1999-2002 sample, the degrees of freedom depend on the number of first stage units, or PSUs, containing observations and is defined as the number of PSUs minus the number of strata. (See Sample Design module for more information.)
The equality of means is usually tested at the .05 level of significance.
References:
Cochran, WG. Sampling Techniques. John Wiley & Sons. 1977.
Lohr SL. Sampling: Design and Analysis. Duxbury Press. Pacific Grove 1999.
In this task, you will use SUDAAN to calculate a t-statistic and assess whether the mean systolic blood pressures (SBP) in males and females age 20 years and older are statistically different.
Step 1: Set Up SUDAAN to Produce Means
Follow the steps in the summary table below to produce the mean SBP using the SUDAAN procedure proc descript.
Important Note: These programs use variable formats listed in the Tutorial Formats page. You may need to format the variables in your dataset the same way to reproduce results presented in the tutorial.
| Statements | Explanation |
|---|---|
|
proc sort data=analysis_data; by sdmvstra sdmvpsu; run ; |
Use the SUDAAN procedure, proc sort, to sort the data by strata (sdmvstra) and PSU (sdmvpsu). |
| proc descript data=analysis_data design=wr; | Use the proc descript procedure to generate means and specify the sample design using the design option WR (with replacement). |
| nest sdmvstra sdmvpsu; | Use the nest statement with strata and PSU to account for the design effects. |
| weight wtmec4yr; | Use the weight statement to account for the unequal probability of sampling and non-response. In this example, the MEC weight for 4 years of data (wtmec4yr) is used. |
| subpopn ridageyr >= 20 ; | Use the subpopn statement to select those 20 years and older.
Because only those 20 years and older are of interest in this example, use the subpopn statement to select this subgroup. Please note that for accurate estimates of the standard error , it is preferable to use subpopn in SUDAAN to select a subgroup for analysis, rather than select the study subgroup in SAS when preparing the data file. (See Section 5.4 of Korn and Graubard Analysis of Data from Health Surveys, pp 207-211.) |
| class riagendr/NoFREQ; | Use a class statement for categorical variables in version 9.0. In earlier versions, you need a subgroup and levels statement. Use the nofreq option to suppress frequencies. |
| var bpxsar; | Use the var statement to choose the continuous variable, systolic blood pressure (bpxsar). |
| print nsum mean semean/style=nchs; | Use the print statement to obtain the N (nsum), mean (mean) and standard error of the mean (semean) for the t-test. |
| rformat riagendr sexfmt. ; | Use the rformat statement to read the SAS formats into SUDAAN. |
| rtitle “Mean systolic blood pressure: NHANES 1999-2002” run ; |
Use the rtitle statement to title the output. |
Step 2: Review SUDAAN Means Output
- 9,056 respondents had information on systolic blood pressure (SBP).
- The results indicate the mean SBP was 124 for males and 122 for females.
Step 3: Perform t-test to Test for Significance
A t-test is used to test whether the mean SBP between males and females obtained in the previous step is statistically significant different.
Request the t-test from the SUDAAN procedure proc descript and follow the steps in the summary table below.
Important Note: Note that this program and the previous program to produce means in Step 1 are identical up to the var statement.
Important Note: These programs use variable formats listed in the Tutorial Formats page. You may need to format the variables in your dataset the same way to reproduce results presented in the tutorial.
| Statements | Explanation |
|---|---|
|
proc sort data =analysis_data; by sdmvstra sdmvpsu; run ; |
Use the SUDAAN procedure, proc sort, to sort the data by strata (sdmvstra) and PSU (sdmvpsu). |
| proc descript data=analysis_data design=wr; | Use the proc descript procedure to generate means and specify the sample design using the design option WR (with replacement). |
| nest sdmvstra sdmvpsu; | Use the nest statement with strata and PSU to account for the design effects. |
| weight wtmec4yr; | Use the weight statement to account for the unequal probability of sampling and non-response. In this example, the MEC weight for 4 years of data (wtmec4yr) is used. |
| subpopn ridageyr >= 20 ; | Use the subpopn statement to select those 20 years and older.
Because only those 20 years and older are of interest in this example, use the subpopn statement to select this subgroup. Please note that for accurate estimates of the standard error , it is preferable to use subpopn in SUDAAN to select a subgroup for analysis, rather than select the study subgroup in the SAS program while preparing the data file. (See Section 5.4 of Korn and Graubard Analysis of Data from Health Surveys, pp 207-211.) |
| class riagendr/NoFREQ; | Use a class statement for categorical variables in version 9.0. In earlier versions, you need a subgroup and levels statement. Use the nofreq option to suppress frequencies. |
| var bpxsar; | Use the var statement to choose the continuous variable, systolic blood pressure. |
| contrast riagendr = ( 1 – 1 )/name = “Males vs. Females” ; | Use the contrast statement to test the hypothesis that the difference equal 0, or mean SBP for males equals the mean SBP for females. |
| print nsum t_mean p_mean/style=nchs; | Use the print statement to obtain the N (nsum), t-test, and p-value for the t-test. |
| rformat riagendr sexfmt. ; | Use the rformat statement to read the SAS formats into SUDAAN. |
| rtitle “Significance test for difference between mean systolic blood pressure for males and females” ; rtitle2 “NHANES 1999-2002” ; |
Use the rtitle statement to title the output. |
Step 4: Review SUDAAN t-test Output
- 9,056 respondents had information on systolic blood pressure where the degrees of freedom was 29.
- To test the hypothesis that the difference between the two means is zero, the t-statistic with 29 degrees of freedom is computed as 2.64. The p-value is 0.0132, which indicates that the probability of obtaining a value of the t-statistic whose absolute value is greater than or equal to 2.64 is 0.0132.
- Therefore, the null hypothesis is rejected at the 0.05 level.
In this task, you will use SAS Survey Procedures to calculate a t-statistic and assess whether the mean systolic blood pressures (SBP) in males and females age 20 years and older are statistically different.
Step 1: Create Variable to Subset Population
In order to subset the data in SAS Survey Procedures, you will need to create a variable for the population of interest. In this example, the sel variable is set to 1 if the sample person is 20 years or older, and 2 if the sample person is younger than 20 years. Then this variable is used in the domain statement to specify the population of interest (those 20 years and older).
if ridageyr GE 20 then sel = 1;
else sel = 2;
Step 2: Set Up SAS Survey Procedures to Produce Means
Follow the explanations in the summary table below to produce the mean SBP using the SAS Survey procedure proc surveymeans.
Information: These programs use variable formats listed in the Tutorial Formats page. You may need to format the variables in your dataset the same way to reproduce results presented in the tutorial.
| Statements | Explanation |
|---|---|
| proc surveymeans data=analysis_data nobs mean stderr; | Use the SAS Survey procedure, proc surveymeans, to count the number of observations (nobs) and calculate means (mean) and standard errors (stderr), and specify the dataset (analysis_data). |
| strata sdmvstra; | Use the strata statement to specify the strata (sdmvstra) and account for design effects of stratification. |
| cluster sdmvpsu; | Use the cluster statement to specify PSU (sdmvpsu) to account for design effects of clustering. |
| class riagendr; | Use the class statement to specify the discrete variables used to select from the subpopulations of interest. In this example, the subpopulation of interest are gender (riagendr). |
| weight wtmec4yr; | Use the weight statement to account for the unequal probability of sampling and non-response. In this example, the MEC weight for 4 years of data (wtmec4yr) is used. |
| domain sel sel*riagendr; | Use the domain statement to select those 20 years and older (sel) by gender (riagendr). Warning: When using proc surveymeans, use a domain statement to select the population of interest. Do not use a where or by-group statement to analyze subpopulations with the SAS Survey Procedures. |
| var bpxsar; | Use the var statement to indicate variable(s) for which descriptive measures are requested. In this example, the systolic blood pressure variable (bpxsar) is used. |
| ods output domain(match_all)=domain; |
Use the ods statement to output the dataset of estimates from the subdomains listed on the domain statement above. This set of commands will output two datasets for each subdomain specified in the domain statement above (domain for sel; domain1 for sel*riagendr). |
| data all; set domain domain1; if sel=1; |
Use the data statement to name the temporary SAS dataset (all) to append the two datasets, created in the previous step, if age is greater than or equal to 20 (sel). |
| proc print; var riagendr n mean stderr; title “Mean systolic blood pressure: NHANES 1999-2002”; run; |
Use the print statement to print the number of observations, the mean, and standard error of the mean in a printer-friendly format. |
Step 3: Review SAS Means Output
- 9,056 respondents had information on systolic blood pressure (SBP).
- The results indicate the mean SBP was 124 for males and 122 for females.
Step 4: Download SAS %sregsub Macro Text File
Because version 9.1 of SAS Survey Procedures for proc surveyreg does not have a domain statement for subpopulation analyses (a domain statement is being added to proc surveyreg in SAS v9.2), you will need to use a macro provided on the SAS website. Download the file, save it to your computer, and make sure to note the location, as you will be referring your SAS program to the file later.
Link to %sregsub macro on SAS website: http://support.sas.com/ctx/samples/index.jsp?sid=483
Step 5: Set up SAS Survey Procedures Macro to Test for Significance
A t-test is used to test whether the mean SBP between males and females obtained in the previous step is statistically significant different.
Request the t-test from the SAS Survey %sregsub macro and follow the steps in the summary table below.
Information: These programs use variable formats listed in the Tutorial Formats page. You may need to format the variables in your dataset the same way to reproduce results presented in the tutorial.
| Statements | Explanation |
|---|---|
| %include ‘C:\NHANES\sample00483_1_sregsub.sas.txt’; | Use the %include function to include the macro text file. In this example, the file is named sample00483_1_sregsub.sas.txt and is saved in the C:\NHANES\ directory. |
| %SREGSUB( | This statement names and opens the macro, %sregsub. |
| DATA= analysis_data, | Use the data statement to call in the dataset (analysis_data). |
| STRATA= sdmvstra, | Use the strata statement to specify the strata (sdmvstra) and account for design effects of stratification. |
| CLUSTER= sdmvpsu, | Use the cluster statement to specify PSU (sdmvpsu) to account for design effects of clustering. |
| CLASS= riagendr, | Use the class statement to specify the discrete variables used to select the subpopulations of interest (i.e., gender [riagendr]. |
| WEIGHT= wtmec4yr, | Use the weight statement to account for the unequal probability of sampling and non-response. In this example, the MEC weight for 4 years of data (wtmec4yr) is used. |
| MODEL= bpxsar = riagendr, | Use a model statement to specify the dependent variable for systolic blood pressure (bpxsar) as a function of the independent variable gender (riagendr). |
| SUBPOP= ridageyr >= 20, | Use the subpop statement to select those 20 years and older. |
| TITLE= ‘Significance test for difference between mean systolic blood pressure for males and females NHANES 1999-2002’ ); |
Use the title statement to label the output. |
Information: The ( ) and the = after the macro parameters, e.g., DATA=, are part of the %sregsub macro
Step 6: Review Output
- 9,056 respondents had information on systolic blood pressure
- The number of degrees of freedom in this example is equal to 29.
- The t-statistic, with 29 degrees of freedom, is equal to 2.64. The p-value of 0.0132 indicates that the probability of obtaining a value of the t-statistic whose absolute value is greater than or equal to 2.64 is 0.0132. Therefore, the null hypothesis is rejected at the 0.05 level.
In this task, you will use SAS Survey Procedures to calculate a t-statistic and assess whether the mean systolic blood pressures (SBP) in males and females age 20 years and older are statistically different.
Step 1: Create Variable to Subset Population
In order to subset the data in SAS Survey Procedures, you will need to create a variable for the population of interest. In this example, the sel variable is set to 1 if the sample person is 20 years or older, and 2 if the sample person is younger than 20 years. Then this variable is used in the domain statement to specify the population of interest (those 20 years and older).
if ridageyr GE 20 then sel = 1;
else sel = 2;
Step 2: Set Up SAS Survey Procedures to Produce Means
Follow the explanations in the summary table below to produce the mean SBP using the SAS Survey procedure proc surveymeans.
Important Note: These programs use variable formats listed in the Tutorial Formats page. You may need to format the variables in your dataset the same way to reproduce results presented in the tutorial.
| Statements | Explanation |
|---|---|
| proc surveymeans data=analysis_data nobs mean stderr; | Use the SAS Survey procedure, proc surveymeans, to count the number of observations (nobs) and calculate means (mean) and standard errors (stderr), and specify the dataset (analysis_data). |
| strata sdmvstra; | Use the strata statement to specify the strata (sdmvstra) and account for design effects of stratification. |
| cluster sdmvpsu; | Use the cluster statement to specify PSU (sdmvpsu) to account for design effects of clustering. |
| class riagendr; | Use the class statement to specify the discrete variables used to select from the subpopulations of interest. In this example, the subpopulation of interest are gender (riagendr). |
| weight wtmec4yr; | Use the weight statement to account for the unequal probability of sampling and non-response. In this example, the MEC weight for 4 years of data (wtmec4yr) is used. |
| domain sel sel*riagendr; | Use the domain statement to select those 20 years and older (sel) by gender (riagendr). Warning: When using proc surveymeans, use a domain statement to select the population of interest. Do not use a where or by-group statement to analyze subpopulations with the SAS Survey Procedures. |
| var bpxsar; | Use the var statement to indicate variable(s) for which descriptive measures are requested. In this example, the systolic blood pressure variable (bpxsar) is used. |
| ods output domain(match_all)=domain; |
Use the ods statement to output the dataset of estimates from the subdomains listed on the domain statement above. This set of commands will output two datasets for each subdomain specified in the domain statement above (domain for sel; domain1 for sel*riagendr). |
| data all; set domain domain1; if sel=1; |
Use the data statement to name the temporary SAS dataset (all) to append the two datasets, created in the previous step, if age is greater than or equal to 20 (sel). |
| proc print; var riagendr n mean stderr; title “Mean systolic blood pressure: NHANES 1999-2002”; run; |
Use the print statement to print the number of observations, the mean, and standard error of the mean in a printer-friendly format. |
Step 3: Review SAS Means Output
- 9,056 respondents had information on systolic blood pressure (SBP).
- The results indicate the mean SBP was 124 for males and 122 for females.
Step 4: Set up SAS Survey Procedures to Test for Significance
A t-test is used to test whether the mean SBP between males and females obtained in the previous step is statistically significant different.
Request the t-test from the SAS Proc Surveyreg procedure and follow the steps in the summary table below.
Important Note: These programs use variable formats listed in the Tutorial Formats page. You may need to format the variables in your dataset the same way to reproduce results presented in the tutorial.
Use SAS %sregsub Macro to Calculate Significance
| Statements | Explanation |
|---|---|
| PROC SURVEYREG DATA=analysis_data nomcar; | Use the SAS Survey procedure, proc surveyreg, to calculate significance. Use the nomcar option to read all observations. |
| STRATA sdmvstra; | Use the strata statement to specify the strata (sdmvstra) and account for design effects of stratification. |
| CLUSTER sdmvpsu; | Use the cluster statement to specify PSU (sdmvpsu) to account for design effects of clustering. |
| CLASS riagendr; | Use the class statement to specify the discrete variables used to select the subpopulations of interest (i.e., gender [riagendr]). |
| WEIGHT wtmec4yr; | Use the weight statement to account for the unequal probability of sampling and non-response. In this example, the MEC weight for 4 years of data (wtmec4yr) is used. |
| DOMAIN sel; | Use the domain statement to specify the subpopulations of interest.
Warning: When using proc surveyreg, use a domain statement to select the population of interest. Do not use a where or by-group statement to analyze subpopulations with the SAS Survey Procedures. |
| MODEL bpxsar = riagendr/ vadjust=none; | Use a model statement to specify the dependent variable for systolic blood pressure (bpxsar) as a function of the independent variable gender (riagendr). The vadjust option specifies whether or not to use variance adjustment. |
| TITLE ‘Significance test for difference between mean systolic blood pressure for males and females NHANES 1999-2002’ | Use the title statement to label the output. |
Step 5: Review Output
- 9,056 respondents had information on systolic blood pressure
- The number of degrees of freedom in this example is equal to 29.
- The t-statistic, with 29 degrees of freedom, is equal to 2.64. The p-value of 0.0132 indicates that the probability of obtaining a value of the t-statistic whose absolute value is greater than or equal to 2.64 is 0.0132. Therefore, the null hypothesis is rejected at the 0.05 level.
In this task, you will use Stata commands to calculate a t-statistic and assess whether the mean systolic blood pressures (SBP) in males and females age 20 years and older are statistically different.
Step 1: Set Up Stata to Produce Means
Follow the steps in the summary table below to produce the mean SBP and the t-test to test whether the mean SBP between males and females obtained is statistically significant different using the Stata command svy:mean.
Warning: There are several things you should be aware of while analyzing NHANES data with Stata. Please see the Stata Tips page to review them before continuing.
Step 2: Use svyset to define survey design variables
Remember that you need to define the SVYSET before using the SVY series of commands. The general format of this command is below:
svyset [w=weightvar], psu(psuvar) strata(stratavar) vce(linearized)
To define the survey design variables for your SBP analysis, use the weight variable for 4 years of MEC data (wtmec4yr), the PSU variable (sdmvpsu), and strata variable (sdmvstra). The vce option specifies the method for calculating the variance and the default is “linearized” which is Taylor linearization. Here is the svyset command for four years of MEC data:
svyset [w= wtmec4yr], psu(sdmvpsu) strata(sdmvstra) vce(linearized)
Step 3: Use svy:mean to generate means and standard errors in Stata
Now, that the svyset has been defined you can use the Stata command, svy: mean, to generate means and standard errors. The general command for obtaining weighted means and standard errors of a subpopulation is below.
svy: mean varname, subpop(if condition)
Use the svy : mean command with the systolic blood pressure variable (bpxsar) to estimate the mean systolic blood pressure for people age 20 years and older. Use the subpop( ) option to select a subpopulation for analysis, rather than select the study population in the Stata program while preparing the data file. This example uses an if statement to define the subpopulation based on the age variable’s (ridageyr) value. Another option is to create a dichotomous variable where the subpopulation of interest is assigned a value of 1, and everyone else is assigned a value of 0.
svy: mean bpxsar, subpop(if ridageyr>=20 & ridageyr<.)
Output of svy:mean

Step 4: Use over option of svy:mean command to generate means and standard errors for different subgroups in Stata
You can also add the over() option to the svy:mean command to generate the means for different subgroups. When you do this, you can type a second command, estat size, to have the output display the subgroup observation numbers. Here is the general format of these commands for this example:
svy: mean varname, subpop(if condition) over(var1 var2)
estat size
Use the svy : mean command with the systolic blood pressure variable (bpxsar) to estimate the mean systolic blood pressure for people age 20 years and older. Use the subpop( ) option to select a subpopulation for analysis, rather than select the study population in the Stata program while preparing the data file. This example uses an if statement to define the subpopulation based on the age variable’s (ridageyr) value. Another option is to create a dichotomous variable where the subpopulation of interest is assigned a value of 1, and everyone else is assigned a value of 0. Use the over option to get stratified results. This example produces estimates by gender. Use the estate size post estimation command to display the number of subpopulation observations and weighted numbers.
svy: mean bpxsar, subpop(if ridageyr>=20 & ridageyr<.) over(riagendr)
estat size, obs size
Output of svy:mean with over option

Step 5a: Test the hypothesis using the lincom post estimation command
If you have already done some estimations, then you can use the lincom command to test the hypothesis that the difference between the mean for the subpopulations equal 0. Use square brackets around the variable you are estimating. After the variables in square brackets, put the stratifier that you want to test (e.g. the variable in the over option). If you used labels for the variable, you can use labels instead of the coded values. Here is the general format of these commands for this example:
lincom [varname]stratval1 – [varname]stratval2
Because you have done some prior estimation, you can use the lincom post estimation command to test the hypothesis that the difference between mean SBP (bpxsar) for males and females equal 0. This example uses labeled values (male, female) instead of the coded values (1,2) for the gender variable (riagendr).
lincom [bpxsar]male – [bpxsar]female
Output of lincom post estimation command

Step 5b: Test the hypothesis using svy:reg command
The svy:reg command could also be used to calculate the t-statistic. The difference between using svy:reg and lincom is that svy:reg can be used without prior estimation. The xi prefix is used before the command to denote a categorical variable and the i prefix before categorical variables. Here is the general format of these commands for this example:
xi: svy, subpop(if condition): reg dependentvar i.varname
Use the svy:reg command with the xi prefix to calculate the t-statistic and assess whether the mean SBP (bpxsar) for males and females age 20 years and older are statistically different. The i prefix denotes the categorical variable, which in this example is riagendr. Use the char function choose the reference group for the categorical variable.
char riagendr[omit]2
xi:svy, subpop(if ridageyr.=20 & ridageyr<.):reg bpxsar i.riagendr,
Output of svy:reg command

Step 6: Review Stata means and t-test output
Here a table summarizing the results of the previous analyses:
| Variable | Subpopulation analyzed | Number of respondents with data | Mean | p value |
|---|---|---|---|---|
| Systolic blood pressure | Adults age 20 and older | 9,056 | 123 | n/a |
| Men age 20 and older | 4,301 | 124 | 0.0132(men vs. women) | |
| Women age 20 and older | 4,755 | 122 |
According to the stratified analysis, men’s mean blood pressure is 2 points higher than women’s. This difference is statistically significant (i.e. a difference this big or bigger would happen just by chance (in a sample of this size) only 1.3% of the time). 9,056 respondents had information on systolic blood pressure (SBP).
In this task, you will use SUDAAN to calculate a t-statistic and assess whether the mean age (ridageyr) for those who are on the 2005 Carrier File aged 65 and older is statistically different comparing participants who are obese (obese=1) and not obese (obese=0).
Step 1: Set Up SUDAAN to Produce Means
Follow the steps in the summary table below to produce the mean age using the SUDAAN procedure proc descript.
Information: These programs use variable formats listed in the Tutorial Formats page. You may need to format the variables in your dataset the same way to reproduce results presented in the tutorial.
| Statements | Explanation |
|---|---|
| proc sort data=DS1; by sdmvstra sdmvpsu; run; |
Use the SUDAAN procedure, proc sort, to sort the data by strata (sdmvstra) and PSU (sdmvpsu). |
| proc descript data=DS1 design=wr; |
Use the proc descript procedure to generate means and specify the sample design using the design option WR (with replacement). |
| nest sdmvstra sdmvpsu; | Use the nest statement with strata (sdmvstra) and PSU (sdmvpsu) to account for the design effects. |
| Weight wt_linkage_adj; | Use the weight statement to account for the unequal probability of sampling and nonresponse. In this example, the adjusted weight for “linkage non-response” is used for six years of data. |
| subpopn ridageyr >= 65 and cms_medicare_match=1 and on_carrier_2005=1; |
Use a subpopn statement to subset on the subgroup of interest. In this example, it selects people aged 65 or older (ridageyr>=65) that linked to the Medicare files at some point during 1999-2007 (CMS_Medicare_match=1) and were on the 2005 Carrier File (on_carrier_2005=1).
Because only those 65 years and older who linked to the 2005 Carrier File are of interest in this example, use the subpopn statement to select this subgroup. Please note that for accurate estimates of the standard error, it is preferable to use subpopn in SUDAAN to select a subgroup for analysis, rather than select the study subgroup in SAS when preparing the data file. (See Section 5.4 of Korn and Graubard Analysis of Data from Health Surveys, pp 207-211.) |
| class obese/NoFREQ; | Use a class statement for categorical variables in version 9.0. In earlier versions, you need a subgroup and levels statement. Use the nofreq option to suppress frequencies. |
| var ridageyr; | Use the var statement to choose the continuous variable, age (ridageyr). |
| print nsum mean semean/style=nchs; | Use the print statement to obtain the N (nsum), mean (mean) and standard error of the mean (semean) for the t-test. |
| rformat obese obese_.; | Use the rformat statement to read the SAS formats into SUDAAN. |
| rtitle “Significance test for difference between mean age for those who were obese vs. not obese and on the 2005 Carrier File: NHANES 1999-2004 linked to Medicare 1999-2007”; run; |
Use the rtitle statement to title the output. |
Step 2: Review SUDAAN Means Output
- The results indicate the mean age was 74.5 for those who were not obese and on the 2005 Carrier File and 72.0 for those who were obese and on the file.
Step 3: Perform t-test to Test for Significance
A t-test is used to test whether the mean age between those who were obese and on the 2005 Carrier File and those who were not obese obtained in the previous step is statistically significant different.
Request the t-test from the SUDAAN procedure proc descript and follow the steps in the summary table below.
Information: Note that this program and the previous program to produce means in Step 1 are identical up to the var statement.
| Statements | Explanation |
|---|---|
| proc sort data=DS1; by sdmvstra sdmvpsu; run; |
Use the SUDAAN procedure, proc sort, to sort the data by strata (sdmvstra) and PSU (sdmvpsu). |
| proc descript data=DS1 design=wr; |
Use the proc descript procedure to generate means and specify the sample design using the design option WR (with replacement). |
| nest sdmvstra sdmvpsu; | Use the nest statement with strata (sdmvstra) and PSU (sdmvpsu) to account for the design effects. |
| Weight wt_linkage_adj; | Use the weight statement to account for the unequal probability of sampling and nonresponse. In this example, the adjusted weight for “linkage non-response” is used for six years of data. |
| subpopn ridageyr >= 65 and cms_medicare_match=1 and on_carrier_2005=1; |
Use a subpopn statement to subset on the subgroup of interest. In this example, it selects people aged 65 or older (ridageyr>=65) that linked to the Medicare files at some point during 1999-2007 (CMS_Medicare_match=1) and were on the 2005 Carrier File (on_carrier_2005=1).
Because only those 65 years and older who linked to the 2005 Carrier File are of interest in this example, use the subpopnstatement to select this subgroup. Please note that for accurate estimates of the standard error, it is preferable to use subpopn in SUDAAN to select a subgroup for analysis, rather than select the study subgroup in SAS when preparing the data file. (See Section 5.4 of Korn and Graubard Analysis of Data from Health Surveys, pp 207-211.) |
| class obese/NoFREQ; | Use a class statement for categorical variables in version 9.0. In earlier versions, you need a subgroup and levels statement. Use the nofreq option to suppress frequencies. |
| var ridageyr; | Use the var statement to choose the continuous variable, age (ridageyr). |
| contrast obese = (1 -1)/name = “obese vs. not”; | Use the contrast statement to test the hypothesis that the difference equal 0, or mean household size for males equals the mean household size for females. |
| print nsum t_mean p_mean/style=nchs; | Use the print statement to obtain the N (nsum), t-test, and p-value for the t-test. |
| rformat obese obese_.; | Use the rformat statement to read the SAS formats into SUDAAN. |
| rtitle “Significance test for difference between mean age for those who were obese and vs. not obese and on 2005 Carrier File”; rtitle2 “NHANES 1999-2004 linked to Medicare 1999-2007”; run; |
Use the rtitle statement to title the output. |
Step 4: Review SUDAAN t-test Output
- 2,095 observations were used in the analysis size where the degrees of freedom were 44.
- To test the hypothesis that the difference between the two means is zero, the t-statistic with 44 degrees of freedom is computed as 8.82. The p-value is <0.01, which indicates that the probability of obtaining a value of the t-statistic whose absolute value is greater than or equal to 8.82 is <0.01.
- Therefore, we reject the null hypothesis at the 0.05 level.
Resources
Korn, E.L. and B.I. Graubard. 1999. Analysis of Health Surveys. New York: Wiley.
Task 2: Perform chi-square test
The chi-square test is used to test the association between two variables cross-classified in a two-way table and the homogeneity of their association.
The chi-square test is used to test the independence of two variables cross classified in a two-way table. (A chi-square statistic with n degrees of freedom is based on a statistic equal to the sum of the squares of n independent normally distributed random variables with mean=0 and unit variance.)
For example, suppose we wished to test the hypothesis that blood pressure cuff size is independent of gender and that we have the following observed frequencies obtained as a result of the cross-classification of blood pressure cuff sizes and gender.
| 1 | 2 | 3 | 4 | Cumulative | |
|---|---|---|---|---|---|
| Men | 63 | 1387 | 2409 | 453 | 4312 |
| Women | 222 | 2065 | 2002 | 493 | 4782 |
| Both genders | 285 | 3452 | 4411 | 946 | 9094 |
In a simple random sample setting (unweighted data), the expected cell frequencies under the null hypothesis that blood pressure cuff size and gender are independent could be obtained by multiplying the marginal total for the jth column by the proportion of individuals in the ith row.
For example, the expected value of blood pressure cuff size 1 for men would be 285*(4312/9094)=135; the expected value of blood pressure cuff size 4 for women would be 946*(4782/9094)=497.
Thus, if Oij = the observed frequency of the ith row and jth column, where i=1,2, … i and j=1,2, … j and
Eij = the expected frequency of the ith row and jth column
Then the formula to test the null hypothesis of independence, using the chi-square statistic, would be
Equation to Test the Null Hypothesis
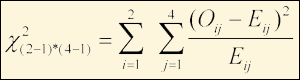 (1)
(1)
This statistic has degrees of freedom equal to the number of rows minus 1, multiplied by the number of columns minus 1.
In a complex sample setting, you would use a statistic similar to equation (1) above, modified to account for survey design with degrees of freedom equal to the number of PSUs minus the number of strata containing observations. This statistic can be obtained through SAS proc surveyfreq (CHISQ, based on the Rao-Scott chi-square with an adjusted F statistic). The analogous procedure in SUDAAN version 9.0 (proc crosstab), provides limited chi-square statistics based on Wald chi-square and does not provide an F adjusted p-value. However, SUDAAN regression models do provide F adjusted chi-square statistics which are recommended for analyzing NHANES data.
The Cochran Mantel Haenzel Test, an extension of the Pearson Chi-Square, can be applied to stratified two-way tables to test for homogeneity or independence in a non-survey setting. For a complex sample its analogue can be obtained in SUDAAN proc crosstab (cmh).
References:
Agresti A. An Introduction to Categorical Data Analysis. Wiley Series in Probability and Statistics. 1996. New York.
In this task, you will use the chi-square test to determine whether gender and blood pressure cuff size are independent of each other.
Step 1: Set Up SUDAAN to Perform Chi-Square Test
The chi-square statistic is requested from the SUDAAN procedure proc crosstab. The summary table below provides an example of how to code for a chi-square test in SUDAAN.
Important Note: These programs use variable formats listed in the Tutorial Formats page. You may need to format the variables in your dataset the same way to reproduce results presented in the tutorial.
| Statements | Explanation |
|---|---|
|
proc sort data =analysis_data;by sdmvstra sdmvpsu; run ; |
Use the SAS procedure, proc sort, to sort the data by strata (sdmvstra) and PSUs(sdmvpsu) before running the procedure in SUDAAN. |
| proc crosstab data=analysis_data design=wr; | Use proc crosstab to examine the relationship between two categorical variables. |
| nest sdmvstra sdmvpsu; | Use the nest statement with strata (sdmvstra) and PSU (sdmvpsu) to account for the design effects. |
| weight wtmec4yr; | Use the weight statement to account for the unequal probability of sampling and non-response. In this example, the MEC weight for 4 years of data (wtmec4yr) is used. |
| subpopn ridageyr >= 20 ; | Use the subpopn statement to select those 20 years and older.
Please note that for accurate estimates of the standard error, it is preferable to use subpopn in SUDAAN to select a subgroup for analysis, rather than select the study subgroup SAS when preparing the data file. (See Section 5.4 of Korn and Graubard Analysis of Data from Health Surveys, pp 207-211). |
| recode bpacsz = (1 3 4 5 ); | Use the recode statement to regroup blood pressure cuff size from five categories to four categories. This collapses the infant and child groups. |
| class riagendr bpacsz/NoFreq; | Use the class statement for categorical variables in version 9.0. In earlier versions, you need a subgroup and levels statement. The NoFreq option suppresses printing frequencies in the output. |
| table riagendr*bpacsz; | Use the table statement to choose the categorical variables gender (riagendr) and blood pressure cuff size (bpacsz) for cross tabulation. |
| print nsum rowper colper/tests=all; | Use the print statement to obtain the N, row percent (rowper),and column percent (colper). Use the tests option to request all available statistics. |
| rformat riagendr sexfmt. ; rformat bpacsz csz1fmt. ; |
Use the rformat statement to read the SAS formats into SUDAAN. |
| rtitle “Chi-square test for blood pressure cuff size: NHANES 1999-2002” ; run ; |
Use the rtitle statement to title the output. |
Important Note: SUDAAN Version 9.0 proc crosstab provides only limited chi-square results (Wald) with p-values based on unadjusted F-statistics (not the recommended statistic for complex survey data). However, the SUDAAN regression procedures do produce the recommended F adjusted chi-square statistics (e.g. Rao-Scott and Satterthwaite) for use in analyzing NHANES data.
Step 2: Review Output
- 9,094 respondents have information on blood pressure cuff size.
- The row percentages indicate that males tend to have a larger cuff size than females.
- Because the p-value is less than 0.05, you would reject the null hypothesis that gender and blood pressure cuff size are independent. The probability of obtaining a value of 274.74 or more is approximately zero.
In this task, you will use the chi-square test in SAS to determine whether gender and blood pressure cuff size are independent of each other.
Step 1: Set Up SAS to Perform Chi-Square Test
The chi-square statistic is requested from the SAS Survey Procedures procedure proc surveyfreq. The summary table below provides an example of how to code for a chi-square test in SAS.
Important Note: These programs use variable formats listed in the Tutorial Formats page. You may need to format the variables in your dataset the same way to reproduce results presented in the tutorial.
| Statements | Explanation |
|---|---|
| proc surveyfreq data=analysis_data; | Use the SAS Survey procedure, proc surveyfreq, to examine the relationship between two categorical variables. |
| strata sdmvstra; | Use the strata statement to specify the strata variable (sdmvstra) and account for design effects of stratification. |
| cluster sdmvpsu; | Use the cluster statement to specify PSU(sdmvpsu) to account for design effects of clustering. |
| weight wtmec4yr; | Use the weight statement to account for the unequal probability of sampling and non-response. In this example, the MEC weight for 4 years of data (wtmec4yr) is used. |
| table sel*riagendr*bpacsz/col row nostd nowt wchisq wllchisq chisq chisq1; | Use the table statement to specify cross-tabulations for which estimates are requested. In the example, the estimates are for age greater than or equal to 20 (sel) by gender (riagendr) and by blood pressure cuff size (bpacsz). The options after the slash will output the column percent (col), row percent (row), Wald chi-square (wchisq), and Wald log linear chi-square (wllchisq), and suppress the standard deviation (nostd) and weighted sums (nowt). Use the chisq option to obtain the Rao-Scott chi-square and the chisq1 to obtain the Rao-Scott modified chi-square. |
| format riagendr sexfmt. bpacsz csz2fmt. ;run ; | Use the format statement to read the SAS formats. |
Important Note: For complex survey data such as NHANES, we recommend using the Rao-Scott F adjusted chi-square statistic since it yields a more conservative interpretation than the Wald chi-square.
Step 2: Review output
- 9,094 respondents have information on blood pressure cuff size.
- The row percentages indicate that males tend to have a larger cuff size than females.
- Because the F adjusted p-value is less than 0.05, you would reject the null hypothesis that gender and blood pressure cuff size are independent. The probability of obtaining a value of 125.55 or more is approximately zero.
In this task, you will use the chi-square test in Stata to determine whether gender and blood pressure cuff size are independent of each other. The chi-square statistics is requested from the Stata command svy:tabulate.
Warning: There are several things you should be aware of while analyzing NHANES data with Stata. Please see the Stata Tips page to review them before continuing.
Step 1: Use svyset to define survey design variables
Remember that you need to define the SVYSET before using the SVY series of commands. The general format of this command is below:
svyset [w=weightvar], psu(psuvar) strata(stratavar) vce(linearized)
To define the survey design variables for your blood pressure cuff size (bpacsz) analysis, use the weight variable for four-yours of MEC data (wtmec4yr), the PSU variable (sdmvpsu), and strata variable (sdmvstra) .The vce option specifies the method for calculating the variance and the default is “linearized” which is Taylor linearization. Here is the svyset command for four years of MEC data:
svyset [w= wtmec4yr], psu(sdmvpsu) strata(sdmvstra) vce(linearized)
Step 2: Regroup blood pressure cuff size variable
In this example, a new variable (cuff_size) is created to regroup blood pressure cuff size (bpacsz) from five categories to four categories. This collapses the infant (1) and child (2) groups. Use the gen command to create a new variable.
gen cuff_size=1 if bpacsz==1 | bpacsz==2
replace cuff_size=2 if bpacsz==3
replace cuff_size=3 if bpacsz==4
replace cuff_size=4 if bpacsz==5
Step 3: Generate chi-square statistics using svy:tabulate
Now, that the svyset has been defined you can use the Stata command, svy: tabulate, to produce two-way tabulations with tests of independence. Some of the options for the tab command include:
- column and row to display column and row percentages (if you do not specify this you will get cell proportions);
- obs lists the number of observations in each cell; count lists the weighted n in each cell and by adding format(%11.0fc) you will display the counts with commas rather than scientific notation;
- ci gives the confidence interval around each estimate, but can only be used with either row or column, not both; and
- the Pearson (Rao-Scott correction F-statistic) chi-square (pearson), null-based (null), and Wald (wald) test statistics.
The general command for generating two-way tabulations is below.
svy:tabulate varname, subpop(if condition) options
Use the svy : tabulate command to produce two-way tabulations for gender (riagendr) and blood pressure cuff size (cuff_size) with tests of independence for people age 20 years and older. (See Section 5.4 of Korn and Graubard Analysis of Data from Health Surveys, pp 207-211). Use the subpop( ) option to select a subpopulation for analysis, rather than select the study population in the Stata program while preparing the data file. This example uses an if statement to define the subpopulation based on the age variable’s (ridageyr) value. Another option is to create a dichotomous variable where the subpopulation of interest is assigned a value of 1, and everyone else is assigned a value of 0. The options specified for this example, use the column, rows, obs, percent, pearson, null and wald test statistic options.
svy:tab riagendr cuff_size, subpop (if ridageyr >=20 & ridageyr<.) column row obs percent pearson null wald
Output of svy:tabulate command with column, row, obs, percent, pearson, null and wald options

Step 4: Review output
Here is a table summarizing the output:
| Variable | Men age 20 and older (n=4312) |
Women age 20 and older (n=4782) |
p value |
|---|---|---|---|
| Cuff size | |||
| (1) Infant | 0% | 0% | <0.0001 |
| (2) Child | 1.5% | 5% | |
| 3 Adult | 29% | 44% | |
| 4 Large | 58% | 41% | |
| 5 Thigh | 12% | 10% |
Men have a larger cuff size than women – for example, 70% of men had cuff size of 4 or 5 compared to 51% of women. Cuff size varies significantly according to gender (p<0.0001). NOTE: The grayed cells have too few observations to create stable estimates and should probably not be reported.
In this task, you will use the chi-square test to determine whether obesity is associated with gender among those who were age 65 and older at the NHANES examination and have claims on the 2005 Carrier File.
Step 1: Set Up SUDAAN to Perform Chi-Square Test
The Chi-square statistic is requested from the SUDAAN procedure proc crosstab. The summary table below provides an example of how to code for a chi-square test in SUDAAN.
Information: These programs use variable formats listed in the Tutorial Formats page. You may need to format the variables in your dataset the same way to reproduce results presented in the tutorial.
| Statements | Explanation |
|---|---|
| proc sort data=DS1; by sdmvstra sdmvpsu;run; |
Use the SAS procedure, proc sort, to sort the data by strata (sdmvstra) and PSUs (sdmvpsu) before running the procedure in SUDAAN. |
| proc crosstab data=DS1 design=wr; | Use proc crosstab to examine the relationship between two categorical variables. |
| nest sdmvstra sdmvpsu; | Use the nest statement with strata (sdmvstra) and PSU (sdmvpsu) to account for the design effects. |
| Weight wt_linkage_adj; | Use the weight statement to account for the unequal probability of sampling and nonresponse. In this example, the adjusted weight for “linkage non-response” is used for six years of data. |
| subpopn ridageyr >= 65 and cms_medicare_match=1 and on_carrier_2005=1; | Use a subpopn statement to subset on the subgroup of interest. In this example, it selects people aged 65 or older (ridageyr>=65) that linked to the Medicare files at some point during 1999-2007 (CMS_Medicare_match=1) and were on the 2005 Carrier File (on_carrier_2005=1). Because only those 65 years and older who linked to the 2005 Carrier File are of interest in this example, use the subpopnstatement to select this subgroup. Please note that for accurate estimates of the standard error, it is preferable to use subpopn in SUDAAN to select a subgroup for analysis, rather than select the study subgroup in SAS when preparing the data file. (See Section 5.4 of Korn and Graubard Analysis of Data from Health Surveys, pp 207-211.) |
| class riagendr obese/NoFreq; | Use the class statement for categorical variables in version 9.0. In earlier versions, you need a subgroup and levels statement. The NoFreq option suppresses printing frequencies in the output. |
| table riagendr*obese; | Use the table statement to choose the categorical variables gender (riagendr) and indicator for being obese (obese) for cross tabulation. |
| print nsum rowper colper/tests=all; | Use the print statement to obtain the N, row percent (rowper),and column percent (colper). Use the tests option to request all available statistics. |
| rformat riagendr sexfmt.; rformat obese obese_.; |
Use the rformat statement to read the SAS formats into SUDAAN. |
| rtitle “Chi-square test for gender by obesity status and on the 2005 Carrier File: NHANES 1999-2004 linked to Medicare 1999-2007”; run; |
Use the rtitle statement to title the output. |
Information: SUDAAN Version 9.0 proc crosstab provides only limited Chi-square results (Wald) with p-values based on unadjusted F-statistics (not the recommended statistic for complex survey data). However, the SUDAAN regression procedures do produce the recommended F adjusted chi-square statistics (e.g. Rao-Scott and Satterthwaite) for use in analyzing NHANES data.
Step 2: Review Output
- 2,095 respondents were included in this analysis.
- The row percentages do not indicate a difference in obesity status by gender for those on the 2005 Carrier File.
- Because the p-value is greater than 0.05, we fail to reject the null hypothesis at the 0.05 level and it is concluded that there is no statistically significant association of obesity and gender for those on the 2005 Carrier File.
Resources
Korn, E.L. and B.I. Graubard. 1999. Analysis of Health Surveys. New York: Wiley.