Data file for the Extended CDC BMI-for-age Growth Charts for Children and Adolescents

The Extended CDC BMI-for-age growth charts use a new method for calculating BMI percentiles and z-scores above the 95th percentile. BMI percentiles and z-scores up to the 95th percentile (z-score 1.645) are the same as those in the 2000 CDC BMI-for-age growth charts and the L,M,S parameters, selected percentiles (3rd, 5th, 10th, 25th, 50th, 75th, 85th, 90th, 95th), and z-scores (-2, -1.5, -.5, 0, .5, 1, 1.5) are identical to those in the data files for the CDC 2000 BMI-for-age growth charts. Newly developed percentiles above the 95th percentile up to the 99.99th percentile (z-scores up to 5), and LMS and sigma parameters for the Extended CDC BMI-for-age growth charts are contained in the following data files.

Selected percentiles and z-scores with LMS and sigma parameters [CSV – 122 KB]

This file contains the L, M, S, and sigma parameters needed to generate exact percentiles and z-scores from the 3^rd to 95^th percentiles by sex (1=male; 2=female) and single month of age. The LMS parameters are the median (M), the generalized coefficient of variation (S), and the power in the Box-Cox transformation (L). Sigma is the dispersion parameter used in the calculation of BMI percentiles and z-scores above the 95^th percentile (z-score 1.645).

Age is listed at the half month point for the entire month; for example, 48.5 months represents 48.0 months up to but not including 49.0 months of age.

Calculate the z-score and corresponding percentile for a given BMI

To obtain a z-score or percentile, first determine if the BMI is above or below the 95^th percentile by comparing it to the sex- and age-specific value of the “P95” column in the data table.

If the BMI is less than or equal to the 95^th percentile:

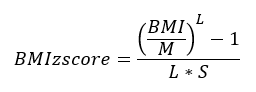
The CDC 2000 BMI z-score is equal to the quotient of BMI divided by the median BMI at the specified sex and age

BMI percentile is equal to the CDF of the BMI z-score multiplied by 100.

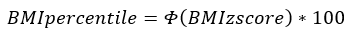
L, M, and S are the values from the data table corresponding to the sex of the child and the age in months. Φ and Φ^-1 are the cumulative distribution function (CDF) of the standard normal distribution and its inverse function. Standard normal distribution tables can be found in statistics textbooks, online sources, and statistical computer programs.

Example:

A girl aged 9 years and 6 months (114.5 months) with BMI = 21.2. For this girl, P95 (95^th percentile) is 22.3979 so her BMI is below the 95^th percentile and L = -2.257782149, M = 16.57626713, and S = 0.132796819.

z-score equal to quotient of 21.2 divided by 16.57 raise to power of -2.257 minus 1 divided by product of -2.257 times 0.132

BMI percentile equals the cumulative distribution function (CDF) of the standard normal distribution of 1.4215 times 100.

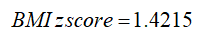
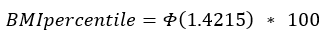
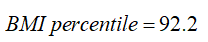
If the BMI is greater than the 95^th percentile:

BMI percentile equals 90 plus 10 times the cumulative distribution function (CDF) of the standard normal distribution

BMI z-score equals the inverse CDF of the standard normal distribution of the quotient of BMI percentile divided by 100.

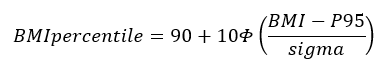
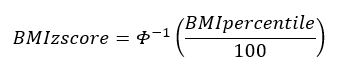
Sigma is the value from the data table corresponding to the sex of the child and the age in months. Φ and Φ^-1 are the cumulative distribution function (CDF) of the standard normal distribution and its inverse function. Standard normal distribution tables can be found in statistics textbooks, online sources, and statistical computer programs.

Example:

A boy aged 4 years and 2 months (50.5 months) with BMI = 22.6. For this boy, P95 (95^th percentile) is 17.8219 so his BMI is above the 95^th percentile and sigma = 2.3983.

BMI percent equals 90 plus 10 times CDF of stand normal distribution of quotient of 22.6 minus 17.8219 divided by 2.398288.

BMI z-score equals the inverse CDF of the standard normal distribution of the quotient of 99.7683 divided by 100.

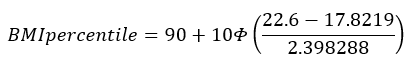
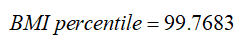
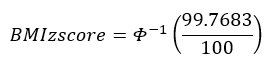
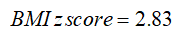
Calculate the BMI for a given z-score or percentile

The calculation of BMI for a given z-score or percentiles up to the 95^th percentile (z = 1.645) is different from its calculation above the 95^th percentile.

If the percentile is less than or equal to 95 or the z-score is less than or equal to 1.645:

BMI equals sex and age-specific median BMI times the quantity 1 plus the product of the sex- and age-specific Box-Cox power

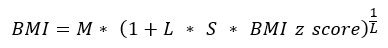
Example:

A girl aged 15 years and 4 months (184.5 months) at a z-score of 1.5 (93.3^rd percentile), which is below the 95^th percentile. L = -2.060616513, M = 20.11172291, and S = 0.150079322.

BMI equals 20.111 times quantity 1 plus product of -2.060 times 0.150 times 1.5 to power of quotient 1 divided by -2.0606165

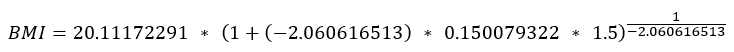
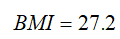
If the percentile is greater than 95 or the z-score is greater than 1.645:

BMI eq inv CDF of stand norm distribute of quote of BMI percent minus 90 divide by 10 multiply by dispers param correspond

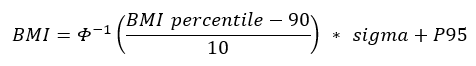
Example:

A boy aged 7 years and 8 months (92.5 months) at the 98.7^th percentile (z-score =2.226), which is above the 95^th percentile. Sigma = 3.8373 and P95 = 19.7477.

BMI equals inverse CDF of stand norm distribute of quotient of 98.7 minus 90 divide by 10 multiply by 3.837343 plus 19.7477

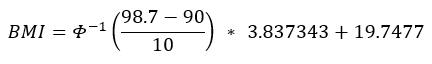
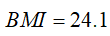
Note on rounding: It is recommended to use all significant digits for intermediate calculations and then round the final result, as appropriate.

To perform the above calculations at age intervals finer than 1 month:

Interpolate L, M, and S values given in the data table
Use the following regression equations to calculate sigma:

Girls:

Sigma equals 0.8334 plus product of 0.3712 times age in years minus the product of 0.0011 times the age in years squared.

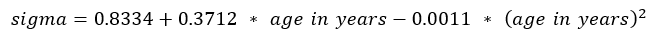
Boys:

Sigma equals 0.3728 plus product of 0.5196 times age in years minus the product of 0.0091 times the age in years squared.

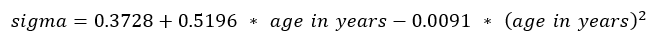
References:

Flegal KM, Cole TJ. Construction of LMS parameters for the Centers for Disease Control and Prevention 2000 growth chart. National health statistics reports; no 63. Hyattsville, MD: National Center for Health Statistics. 2013.
Wei R, Ogden CL, Parsons VL, Freedman DS, Hales CM. A method for calculating BMI z-scores and percentiles above the 95th percentile of the CDC growth charts. Ann Hum Biol. 2020 Sep;47(6):514-521.